
Dear Scientific American,
After reading your Mathematical Recreations in your August 1999 issue about Sierpinski's Gasket, I remembered that about 3 years ago I was very interested in this very same fractal after watching a program on PBS about Chaos and Fractals.
Being an algorithm developer, I quickly implemented a computer program to generate Sierpinski's Gasket using the method of selecting one of the three vertices at random, and making a new point by bisecting the line between the previous point and the selected vertex. Performing this iteration over and over again produced Sierpinski's gasket.

I then wondered if this method would work for other "n" sided regular polygons, where "n" is greater than 3. So I immediately generalized the program for "n" sided polygons, and generated several plots using the "half the distance" rule. Unfortunately, this led me down the "numerical-garden-path", producing very non-interesting results.
Shortly thereafter, I decided to look at another regular polygon, specifically the pentagon. Why? Because I'm a particular fan of "The Golden Section", or "The Golden Mean". The pentagon was a natural choice, because it's geometry is filled with "the Golden Section". So I decided to adapt my program to use the Golden Section. Instead of dividing the distance to the next vertex by 2, I divided the distance by the golden section (Å 1.6180340). To my delight, it worked! I generated a new fractal based on pentagons.

If it doesn't have a name already, I'd like to call it "The Military Gasket", because of it's resemblance to a famous military building, and in mathematical terms, this figure, like other fractals contains little or no information at all other than itself.
Now, the next step was to generalize what "The Golden Section" is to a pentagon, to an "n" sided polygon. So, referring to Figure 1, I knew that line segment CD represented the inverse of "The Golden Section" given that any side of the pentagon (line segment AB) is of unit length.
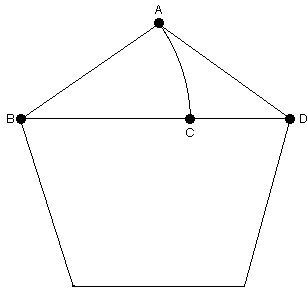
fig. 1
Working it out, for an "n" sided polygon, I got :
This yielded the following plots for n = 6, 7, 8, and 9 :

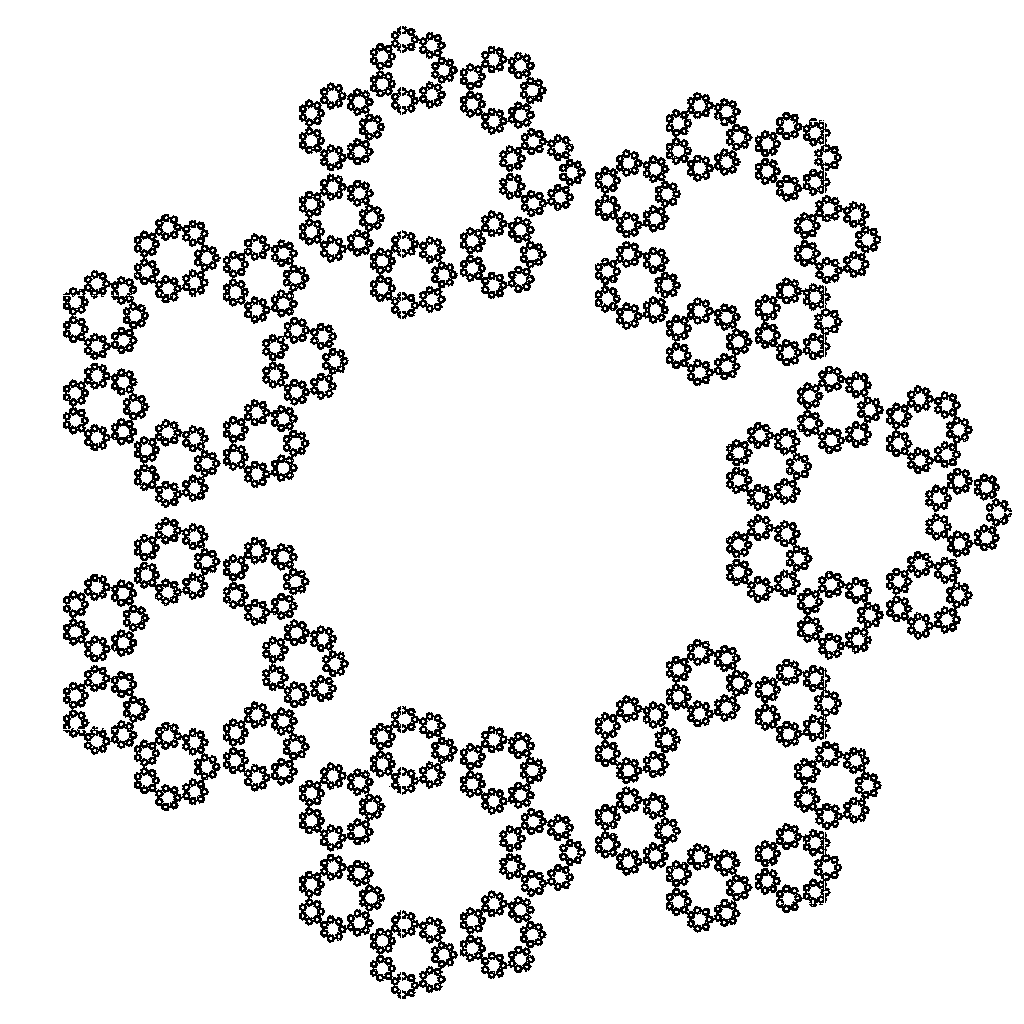
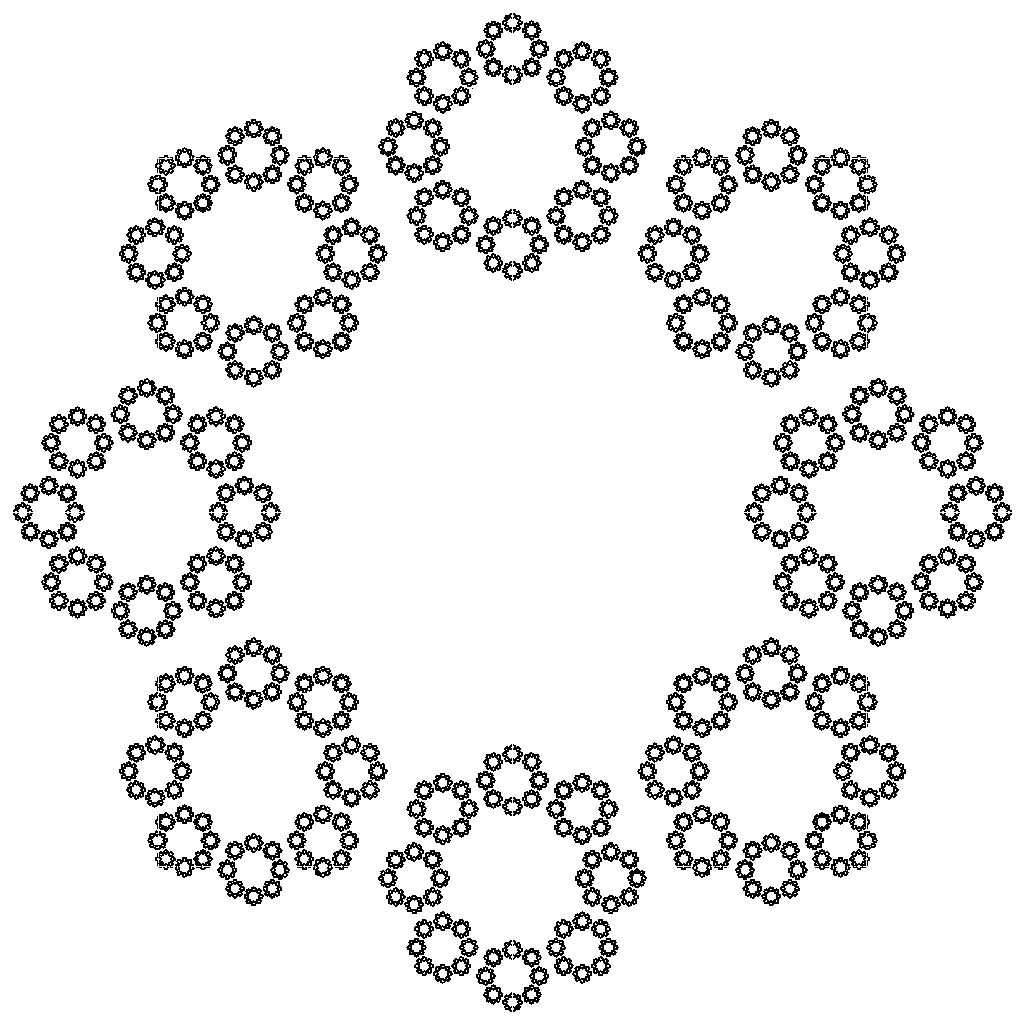

It also yielded a regular pattern for "n" = 4, or a square, although the results were not as interesting :
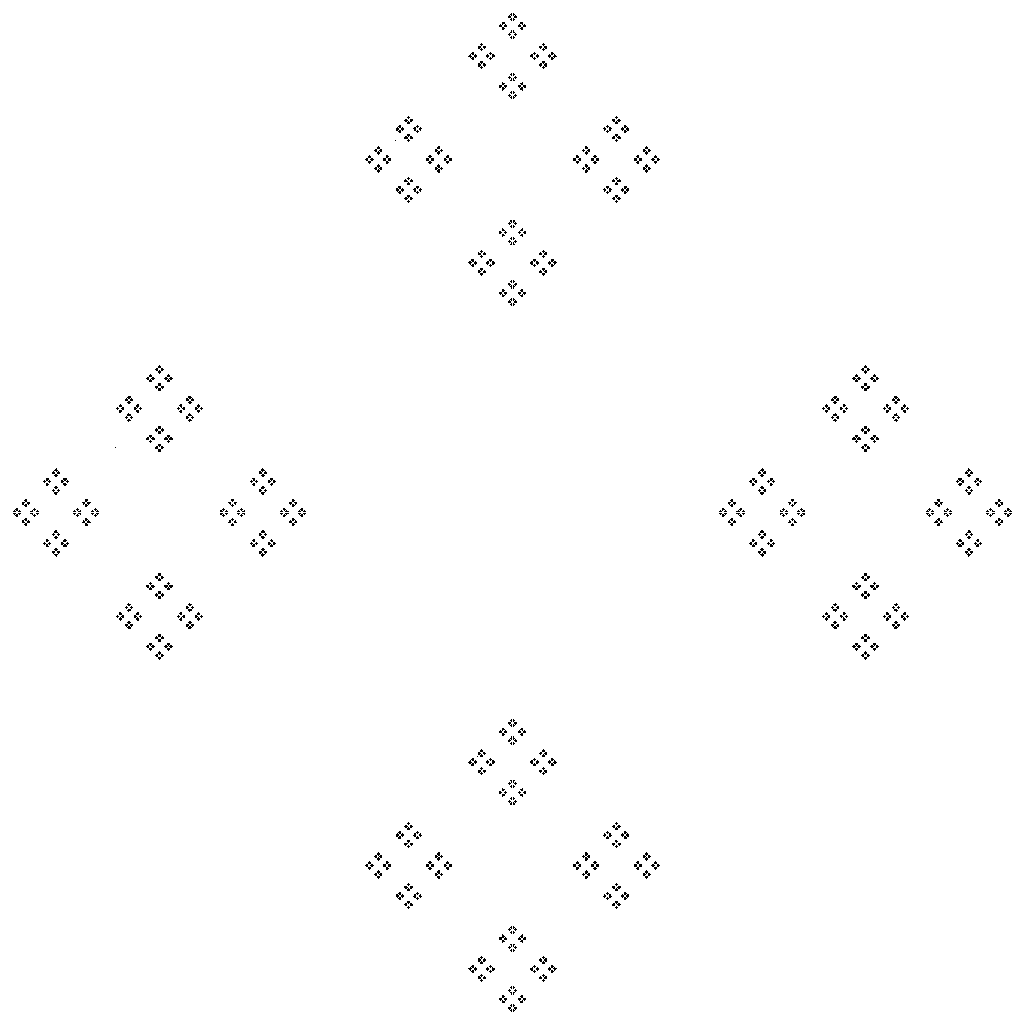
While in each of the above fractals, the hexagons are made up of minor hexagons, the heptagons are made of minor heptagons, and the octagons are made up of octagons, etcetera. I don't think this is the proper solution just yet. If you look closely at the pentagon fractal, each minor pentagon is tangent to each other pentagon. However in the hexagon fractal, each minor hexagon slightly overlays it's neighbor, and for some values of "n" like 7, 8 and 9, the neighboring polygons do not touch. I also tested "n" = 32, and "n" = 64 only to find that the polygons intersect again.
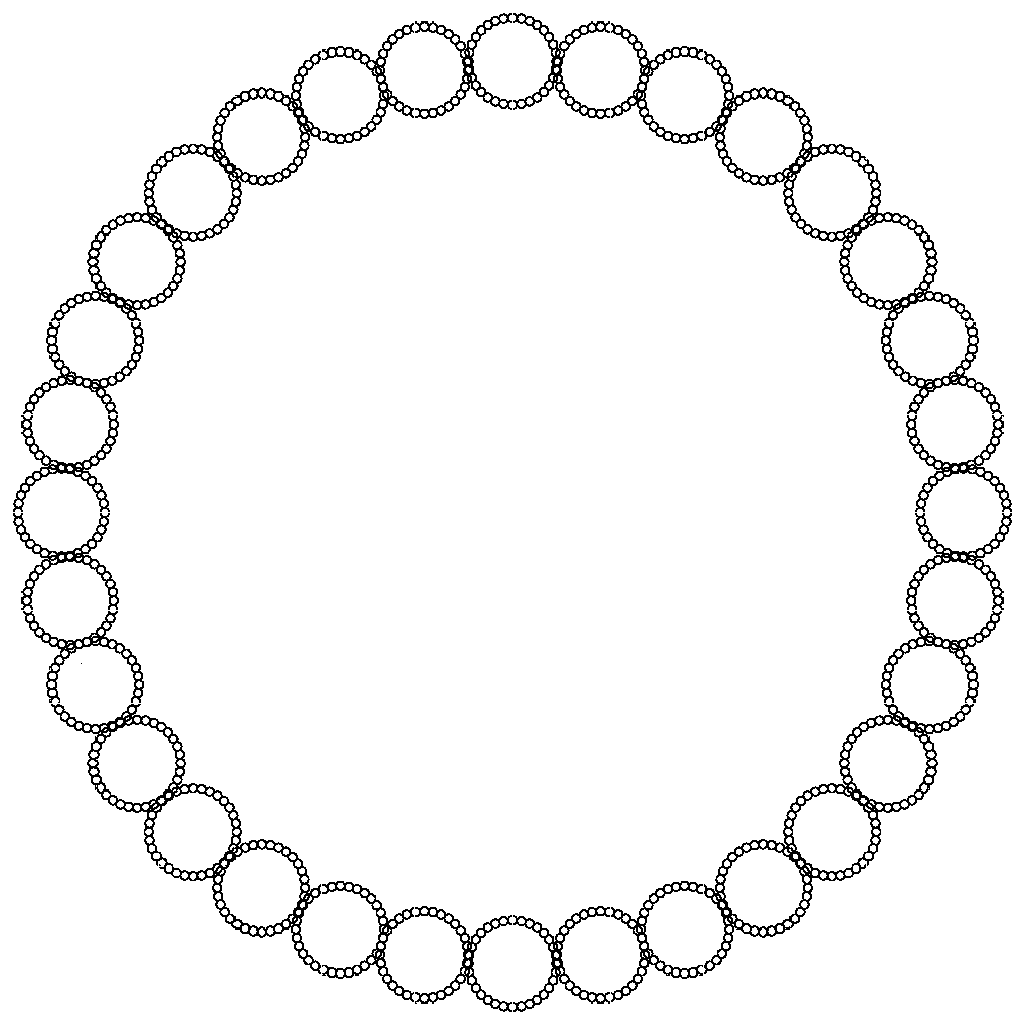

It's also easy to determine, by experiment, and by taking the limit of the equation as "n" approaches infinity, that the resulting figure becomes a circle made up infinitesimal circles.
If anyone is interested in the FORTRAN source program that generated these fractals, they can be found on my website at http://www.jcameron.com/vms/source/POLYFRAC.FOR.
Sincerely
Jeff Cameron
PS. Each of the above fractal images is actually a 1024 by 1024 GIF image, and compressed to a smaller size just for presentation on this page. Looking at each of the original files provided, using a picture viewing program, you can zoom up and see that each polygon goes 5 maybe 6 generations deep before they start to loose resolution.